跳转到->Codeforces Round #753 (Div. 3)〰
A. Linear Keyboard
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output
You are given a keyboard that consists of 2626 keys. The keys are arranged sequentially in one row in a certain order. Each key corresponds to a unique lowercase Latin letter.
You have to type the word ss on this keyboard. It also consists only of lowercase Latin letters.
To type a word, you need to type all its letters consecutively one by one. To type each letter you must position your hand exactly over the corresponding key and press it.
Moving the hand between the keys takes time which is equal to the absolute value of the difference between positions of these keys (the keys are numbered from left to right). No time is spent on pressing the keys and on placing your hand over the first letter of the word.
For example, consider a keyboard where the letters from ‘a’ to ‘z’ are arranged in consecutive alphabetical order. The letters ‘h’, ‘e’, ‘l’ and ‘o’ then are on the positions 88, 55, 1212 and 1515, respectively. Therefore, it will take |5−8|+|12−5|+|12−12|+|15−12|=13|5−8|+|12−5|+|12−12|+|15−12|=13 units of time to type the word “hello”.
Determine how long it will take to print the word ss.
Input
The first line contains an integer tt (1≤t≤10001≤t≤1000) — the number of test cases.
The next 2t2t lines contain descriptions of the test cases.
The first line of a description contains a keyboard — a string of length 2626, which consists only of lowercase Latin letters. Each of the letters from ‘a’ to ‘z’ appears exactly once on the keyboard.
The second line of the description contains the word ss. The word has a length from 11 to 5050 letters inclusive and consists of lowercase Latin letters.
Output
Print tt lines, each line containing the answer to the corresponding test case. The answer to the test case is the minimal time it takes to type the word ss on the given keyboard.
Example
input
Copy
5
abcdefghijklmnopqrstuvwxyz
hello
abcdefghijklmnopqrstuvwxyz
i
abcdefghijklmnopqrstuvwxyz
codeforces
qwertyuiopasdfghjklzxcvbnm
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qwertyuiopasdfghjklzxcvbnm
abacaba
output
Copy
13
0
68
0
74
代码与解释
无脑直接暴力即可
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb push_back
#define ppb pop_back
#define lbnd lower_bound
#define ubnd upper_bound
#define endl '\n'
#define trav(a, x) for(auto& a : x)
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (ll)x.size()
#define hell 1000000007
#define DEBUG cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x) trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x) cerr << #x << " is " << x << endl;
#define ini(a) memset(a,0,sizeof(a))
#define case ll T;read(T);for(ll Q=1;Q<=T;Q++)
#define lowbit(x) x&(-x)
#define pr printf
#define sc scanf
#define _ 0
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \
(void)(cout << "L" << __LINE__ \
<< ": " << #x << " = " << (x) << '\n')
#define TIE \
cin.tie(0);cout.tie(0);\
ios::sync_with_stdio(false);
//#define long long int
//using namespace __gnu_pbds;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
inline void write(long long x) {
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
putchar('\n');
}
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int maxn = 1009;
const ll N = 5;
const double inf=1e20;
const double eps=1e-8;
const double pi=acos(-1.0);
const int maxp=1010;
string a,b;
int fun(char x) {
for (int i=0; i<a.size(); i++) {
if (x == a[i]) {
return i;
}
}
}
void solve(){
cin>>a>>b;
int ans = 0;
for (int i=1; i<b.size(); i++) {
ans += abs(fun(b[i]) - fun(b[i-1]));
}
cout<<ans<<endl;
}
int main()
{
// TIE;
// solve();
case{solve();}
// case{cout<<"Case "<<Q<<":"<<endl;solve();}
}
B. Odd Grasshopper
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output
The grasshopper is located on the numeric axis at the point with coordinate x0x0.
Having nothing else to do he starts jumping between integer points on the axis. Making a jump from a point with coordinate xx with a distance dd to the left moves the grasshopper to a point with a coordinate x−dx−d, while jumping to the right moves him to a point with a coordinate x+dx+d.
The grasshopper is very fond of positive integers, so for each integer ii starting with 11 the following holds: exactly ii minutes after the start he makes a jump with a distance of exactly ii. So, in the first minutes he jumps by 11, then by 22, and so on.
The direction of a jump is determined as follows: if the point where the grasshopper was before the jump has an even coordinate, the grasshopper jumps to the left, otherwise he jumps to the right.
For example, if after 1818 consecutive jumps he arrives at the point with a coordinate 77, he will jump by a distance of 1919 to the right, since 77 is an odd number, and will end up at a point 7+19=267+19=26. Since 2626 is an even number, the next jump the grasshopper will make to the left by a distance of 2020, and it will move him to the point 26−20=626−20=6.
Find exactly which point the grasshopper will be at after exactly nn jumps.
Input
The first line of input contains an integer tt (1≤t≤1041≤t≤104) — the number of test cases.
Each of the following tt lines contains two integers x0x0 (−1014≤x0≤1014−1014≤x0≤1014) and nn (0≤n≤10140≤n≤1014) — the coordinate of the grasshopper’s initial position and the number of jumps.
Output
Print exactly tt lines. On the ii-th line print one integer — the answer to the ii-th test case — the coordinate of the point the grasshopper will be at after making nn jumps from the point x0x0.
Example
input
Copy
9
0 1
0 2
10 10
10 99
177 13
10000000000 987654321
-433494437 87178291199
1 0
-1 1
output
Copy
-1
1
11
110
190
9012345679
-87611785637
1
0
Note
The first two test cases in the example correspond to the first two jumps from the point x0=0x0=0.
Since 00 is an even number, the first jump of length 11 is made to the left, and the grasshopper ends up at the point 0−1=−10−1=−1.
Then, since −1−1 is an odd number, a jump of length 22 is made to the right, bringing the grasshopper to the point with coordinate −1+2=1−1+2=1.
代码与解释
找规律,如果是偶数,假设从0开始,那么
0 -1 1 4 0 -5 1 8 …
可以观察规律,只要%4=0,那么就是0,%4=2,就是1
剩下的%1的是-1,-5,-9…,%3的是4,8,12…
这样规律就出来了
奇数也是类似如此
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb push_back
#define ppb pop_back
#define lbnd lower_bound
#define ubnd upper_bound
#define endl '\n'
#define trav(a, x) for(auto& a : x)
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (ll)x.size()
#define hell 1000000007
#define DEBUG cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x) trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x) cerr << #x << " is " << x << endl;
#define ini(a) memset(a,0,sizeof(a))
#define case ll T;read(T);for(ll Q=1;Q<=T;Q++)
#define lowbit(x) x&(-x)
#define pr printf
#define sc scanf
#define _ 0
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \
(void)(cout << "L" << __LINE__ \
<< ": " << #x << " = " << (x) << '\n')
#define TIE \
cin.tie(0);cout.tie(0);\
ios::sync_with_stdio(false);
//#define long long int
//using namespace __gnu_pbds;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
inline void write(long long x) {
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
putchar('\n');
}
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int maxn = 1009;
const ll N = 5;
const double inf=1e20;
const double eps=1e-8;
const double pi=acos(-1.0);
const int maxp=1010;
void solve(){
ll a,b;
cin>>a>>b;
if (a&1) {
if (b % 4 == 0) {
cout<<a<<endl;
} else if (b % 4 == 2) {
cout<<a-1<<endl;
} else if (b % 4 == 1) {
ll x = b/4;
ll y = 4*x + 1;
cout<<a+y<<endl;
} else if (b % 4 == 3){
ll x = b/4;
ll y = (-4)*x -4;
cout<<a + y<<endl;
}
} else {
if (b % 4 == 0) {
cout<<a<<endl;
} else if (b % 4 == 2) {
cout<<a+1<<endl;
} else if (b % 4 == 1) {
ll x = b/4;
ll y = (-4)*x -1;
cout<<a + y<<endl;
} else if (b % 4 == 3){
ll x = b/4;
ll y = 4*x + 4;
cout<<a+y<<endl;
}
}
}
int main()
{
// TIE;
// solve();
case{solve();}
// case{cout<<"Case "<<Q<<":"<<endl;solve();}
}
C. Minimum Extraction
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output
Yelisey has an array aa of nn integers.
If aa has length strictly greater than 11, then Yelisei can apply an operation called minimum extraction to it:
- First, Yelisei finds the minimal number mm in the array. If there are several identical minima, Yelisey can choose any of them.
- Then the selected minimal element is removed from the array. After that, mm is subtracted from each remaining element.
Thus, after each operation, the length of the array is reduced by 11.
For example, if a=[1,6,−4,−2,−4]a=[1,6,−4,−2,−4], then the minimum element in it is a3=−4a3=−4, which means that after this operation the array will be equal to a=[1−(−4),6−(−4),−2−(−4),−4−(−4)]=[5,10,2,0]a=[1−(−4),6−(−4),−2−(−4),−4−(−4)]=[5,10,2,0].
Since Yelisey likes big numbers, he wants the numbers in the array aa to be as big as possible.
Formally speaking, he wants to make the minimum of the numbers in array aa to be maximal possible (i.e. he want to maximize a minimum). To do this, Yelisey can apply the minimum extraction operation to the array as many times as he wants (possibly, zero). Note that the operation cannot be applied to an array of length 11.
Help him find what maximal value can the minimal element of the array have after applying several (possibly, zero) minimum extraction operations to the array.
Input
The first line contains an integer tt (1≤t≤1041≤t≤104) — the number of test cases.
The next 2t2t lines contain descriptions of the test cases.
In the description of each test case, the first line contains an integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the original length of the array aa. The second line of the description lists nn space-separated integers aiai (−109≤ai≤109−109≤ai≤109) — elements of the array aa.
It is guaranteed that the sum of nn over all test cases does not exceed 2⋅1052⋅105.
Output
Print tt lines, each of them containing the answer to the corresponding test case. The answer to the test case is a single integer — the maximal possible minimum in aa, which can be obtained by several applications of the described operation to it.
Example
input
Copy
8
1
10
2
0 0
3
-1 2 0
4
2 10 1 7
2
2 3
5
3 2 -4 -2 0
2
-1 1
1
-2
output
Copy
10
0
2
5
2
2
2
-2
Note
In the first example test case, the original length of the array n=1n=1. Therefore minimum extraction cannot be applied to it. Thus, the array remains unchanged and the answer is a1=10a1=10.
In the second set of input data, the array will always consist only of zeros.
In the third set, the array will be changing as follows: [−1,2,0]→[3,1]→[2][−1,2,0]→[3,1]→[2]. The minimum elements are highlighted with blueblue. The maximal one is 22.
In the fourth set, the array will be modified as [2,10,1,7]→[1,9,6]→[8,5]→[3][2,10,1,7]→[1,9,6]→[8,5]→[3]. Similarly, the maximum of the minimum elements is 55.
代码与解释
题意是找到最小的数字,然后在数组中去掉这个数字,并且所有数字都减去这个最小的数字,问可能的最大的最小数字是多少
写法是可以找到最大的差值,然后对比现在最小的,取大的即可
为什么找最大的差值?因为要找到最大的最小数字,假设1,4,7,那么减去1,就是3,6,再减去3,就是3和7-4的值一样,最后再对比现在最小的即可
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb push_back
#define ppb pop_back
#define lbnd lower_bound
#define ubnd upper_bound
#define endl '\n'
#define trav(a, x) for(auto& a : x)
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (ll)x.size()
#define hell 1000000007
#define DEBUG cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x) trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x) cerr << #x << " is " << x << endl;
#define ini(a) memset(a,0,sizeof(a))
#define case ll T;read(T);for(ll Q=1;Q<=T;Q++)
#define lowbit(x) x&(-x)
#define pr printf
#define sc scanf
#define _ 0
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \
(void)(cout << "L" << __LINE__ \
<< ": " << #x << " = " << (x) << '\n')
#define TIE \
cin.tie(0);cout.tie(0);\
ios::sync_with_stdio(false);
//#define long long int
//using namespace __gnu_pbds;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
inline void write(long long x) {
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
putchar('\n');
}
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int maxn = 2e5+10;
const ll N = 5;
vector<int> vi;
vector<int> vi2;
bool cmp(int a, int b) {
return a>b;
}
void solve(){
vi.clear();
vi2.clear();
int t, q;
cin>>t;
if (t == 1) {
cin>>q;
cout<<q<<endl;
return;
}else
for (int i=0; i<t; i++) {
cin>>q;
vi.pb(q);
}
sort(all(vi));
int maxx = 0;
for (int i=0; i<vi.size()-1; i++) {
maxx = max(vi[i+1] - vi[i], maxx);
}
if (maxx > vi[0])
cout<<maxx<<endl;
else
cout<<vi[0]<<endl;
}
int main()
{
// TIE;
// solve();
case{solve();}
// case{cout<<"Case "<<Q<<":"<<endl;solve();}
}
D. Blue-Red Permutation
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output
You are given an array of integers aa of length nn. The elements of the array can be either different or the same.
Each element of the array is colored either blue or red. There are no unpainted elements in the array. One of the two operations described below can be applied to an array in a single step:
- either you can select any blue element and decrease its value by 11;
- or you can select any red element and increase its value by 11.
Situations in which there are no elements of some color at all are also possible. For example, if the whole array is colored blue or red, one of the operations becomes unavailable.
Determine whether it is possible to make 00 or more steps such that the resulting array is a permutation of numbers from 11 to nn?
In other words, check whether there exists a sequence of steps (possibly empty) such that after applying it, the array aa contains in some order all numbers from 11 to nn (inclusive), each exactly once.
Input
The first line contains an integer tt (1≤t≤1041≤t≤104) — the number of input data sets in the test.
The description of each set of input data consists of three lines. The first line contains an integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the length of the original array aa. The second line contains nn integers a1a1, a2a2, …, anan (−109≤ai≤109−109≤ai≤109) — the array elements themselves.
The third line has length nn and consists exclusively of the letters ‘B’ and/or ‘R’: iith character is ‘B’ if aiai is colored blue, and is ‘R’ if colored red.
It is guaranteed that the sum of nn over all input sets does not exceed 2⋅1052⋅105.
Output
Print tt lines, each of which contains the answer to the corresponding test case of the input. Print YES as an answer if the corresponding array can be transformed into a permutation, and NO otherwise.
You can print the answer in any case (for example, the strings yEs, yes, Yes, and YES will be recognized as a positive answer).
Example
input
Copy
8
4
1 2 5 2
BRBR
2
1 1
BB
5
3 1 4 2 5
RBRRB
5
3 1 3 1 3
RBRRB
5
5 1 5 1 5
RBRRB
4
2 2 2 2
BRBR
2
1 -2
BR
4
-2 -1 4 0
RRRR
output
Copy
YES
NO
YES
YES
NO
YES
YES
YES
Note
In the first test case of the example, the following sequence of moves can be performed:
- choose i=3i=3, element a3=5a3=5 is blue, so we decrease it, we get a=[1,2,4,2]a=[1,2,4,2];
- choose i=2i=2, element a2=2a2=2 is red, so we increase it, we get a=[1,3,4,2]a=[1,3,4,2];
- choose i=3i=3, element a3=4a3=4 is blue, so we decrease it, we get a=[1,3,3,2]a=[1,3,3,2];
- choose i=2i=2, element a2=2a2=2 is red, so we increase it, we get a=[1,4,3,2]a=[1,4,3,2].
We got that aa is a permutation. Hence the answer is YES.
代码与解释
两组数,red和blue组,然后分开进行判定
两组先排序
blue因为不能增加,所以从小到大从1开始判定,每次num++,大于等于num就是正常的,否则输出NO(这行的意思其实就是判定从1开始每个数字是否都能取,下面那行是从n开始前面的数字是否能取)
red因为不能减少,所以从大开始筛选,每次判定正常(<=)之后num—,否则输出NO
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb push_back
#define ppb pop_back
#define lbnd lower_bound
#define ubnd upper_bound
#define endl '\n'
#define trav(a, x) for(auto& a : x)
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (ll)x.size()
#define hell 1000000007
#define DEBUG cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x) trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x) cerr << #x << " is " << x << endl;
#define ini(a) memset(a,0,sizeof(a))
#define case ll T;read(T);for(ll Q=1;Q<=T;Q++)
#define lowbit(x) x&(-x)
#define pr printf
#define sc scanf
//#define _ 0
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \
(void)(cout << "L" << __LINE__ \
<< ": " << #x << " = " << (x) << '\n')
#define TIE \
cin.tie(0);cout.tie(0);\
ios::sync_with_stdio(false);
//#define long long int
//using namespace __gnu_pbds;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
inline void write(long long x) {
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
putchar('\n');
}
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pi = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int maxn = 200009;
const ll N = 5;
int arr[maxn];
bool cmp(int a,int b) {
return a>b;
}
void solve(){
int t;
string s;
vector<int> b,r;
cin>>t;
for (int i=0; i<t; i++) cin>>arr[i];
cin>>s;
for (int i=0; i<s.size(); i++) {
if (s[i] == 'B') b.pb(arr[i]);
else r.pb(arr[i]);
}
sort(all(b));
sort(all(r),cmp);
int num = 1;
for (int i=0; i<b.size(); i++) {
if (b[i] >= num) {
num++;
} else {
cout<<"NO"<<endl;
return ;
}
}
num = t;
for (int i=0; i<r.size(); i++) {
if (r[i] <= num) {
num--;
} else {
cout<<"NO"<<endl;
return ;
}
}
cout<<"YES"<<endl;
}
int main()
{
// TIE;
#ifndef ONLINE_JUDGE
// freopen ("in.txt" , "r", stdin );
// freopen ("out.txt", "w", stdout);
#else
#endif
// solve();
case{solve();}
// case{cout<<"Case "<<Q<<":"<<endl;solve();}
// return ~~(0^_^0);
}
E. Robot on the Board 1
time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output
The robot is located on a checkered rectangular board of size n×mn×m (nn rows, mm columns). The rows in the board are numbered from 11 to nn from top to bottom, and the columns — from 11 to mm from left to right.
The robot is able to move from the current cell to one of the four cells adjacent by side.
The sequence of commands ss executed by the robot is given. Each command is denoted by one of the symbols ‘L’, ‘R’, ‘D’ or ‘U’, and triggers the movement to left, right, down or up, respectively.
The robot can start its movement in any cell. The robot executes the commands starting from the first one, strictly in the order in which they are listed in ss. If the robot moves beyond the edge of the board, it falls and breaks. A command that causes the robot to break is not considered successfully executed.
The robot’s task is to execute as many commands as possible without falling off the board. For example, on board 3×3, if the robot starts a sequence of actions s=s=“RRDLUU” (“right”, “right”, “down”, “left”, “up”, “up”) from the central cell, the robot will perform one command, then the next command will force him to cross the edge. If the robot starts moving from the cell (2,1) (second row, first column) then all commands will be executed successfully and the robot will stop at the cell (1,2) (first row, second column).
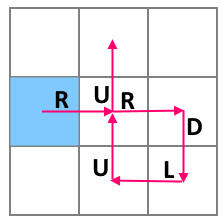The robot starts from cell (2,1) (second row, first column). It moves right, right, down, left, up, and up. In this case it ends in the cell (1,2)((first row, second column).
Determine the cell from which the robot should start its movement in order to execute as many commands as possible.
Input
The first line contains an integer t(1≤t≤104) — the number of test cases.
The next 2t lines contain descriptions of the test cases.
In the description of each test case, the first line contains two integers nn and mm (1≤n,m≤1061≤n,m≤106) — the height and width of the field that the robot is located on. The second line of the description is a string ss consisting solely of characters ‘L’, ‘R’, ‘D’ and ‘U’ — the sequence of commands the robot executes. The string has a length from 11 to 106106 commands.
It is guaranteed that the total length of ss over all test cases does not exceed 106106.
Output
Print t lines, each of which contains the answer to the corresponding test case. The answer to the test case are two integers r (1≤r≤n) and cc (1≤c≤m), separated by a space — the coordinates of the cell (row number and column number) from which the robot should start moving to perform as many commands as possible.
If there are several such cells, you may output any of them.
Example
input
Copy
4
1 1
L
1 2
L
3 3
RRDLUU
4 3
LUURRDDLLLUU
output
Copy
1 1
1 2
2 1
3 2
代码与解释
参考了网上大佬的代码,也不算难,一个简单的模拟,判断边界,然后移动起始坐标
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb push_back
#define ppb pop_back
#define lbnd lower_bound
#define ubnd upper_bound
#define endl '\n'
#define trav(a, x) for(auto& a : x)
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (ll)x.size()
#define hell 1000000007
#define DEBUG cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x) trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x) cerr << #x << " is " << x << endl;
#define ini(a) memset(a,0,sizeof(a))
#define case ll T;read(T);for(ll Q=1;Q<=T;Q++)
#define lowbit(x) x&(-x)
#define pr printf
#define sc scanf
//#define _ 0
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \
(void)(cout << "L" << __LINE__ \
<< ": " << #x << " = " << (x) << '\n')
#define TIE \
cin.tie(0);cout.tie(0);\
ios::sync_with_stdio(false);
//#define long long int
//using namespace __gnu_pbds;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
inline void write(long long x) {
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
putchar('\n');
}
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pi = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int maxn = 200009;
const ll N = 5;
void solve(){
int n, m;
string s;
cin>>n>>m>>s;
int dx = 0, dy = 0;
int minx = 0, miny = 0;
int maxx = 0,maxy = 0;
int ansx = 1, ansy = 1;
for (auto it : s) {
if (it == 'L') dx --;
else if (it == 'R') dx ++;
else if (it == 'U') dy --;
else if (it == 'D') dy ++;
minx = min(minx,dx);
miny = min(miny,dy);
maxx = max(maxx,dx);
maxy = max(maxy,dy);
if ((maxx - minx) >= m || (maxy - miny) >= n) break;//越界就结束
ansx = 1 - minx;//minx最大肯定是0(所以初始化为0),如果有小于0的就反加上,下面miny类似
ansy = 1 - miny;
}
cout<<ansy<<" "<<ansx<<endl;
}
int main()
{
// TIE;
#ifndef ONLINE_JUDGE
// freopen ("in.txt" , "r", stdin );
// freopen ("out.txt", "w", stdout);
#else
#endif
// solve();
case{solve();}
// case{cout<<"Case "<<Q<<":"<<endl;solve();}
// return ~~(0^_^0);
}