leetcode 第 391 场周赛
March 31, 2024
6 min read
#算法
#cpp
前三道只放一下代码,比较简单,重点是第四道,我没写出来
哈沙德数
class Solution {
public:
int sumOfTheDigitsOfHarshadNumber(int x) {
int sum = 0;
int xx = x;
while (x > 0) {
sum += x % 10;
x /= 10;
}
if (xx % sum == 0) return sum;
return -1;
}
};换水问题 II
class Solution {
public:
int maxBottlesDrunk(int numBottles, int numExchange) {
int ans = numBottles;
while (numBottles >= numExchange) {
numBottles -= numExchange;
numExchange ++;
ans ++;
numBottles ++;
cout << numBottles << " " << numExchange << endl;
}
return ans;
}
};交替子数组计数
双指针,每次选择最长的交替子数组然后计算
class Solution {
// 找到最小的子数组,然后算A
public:
long long A(long long x) {
return x * (x + 1) / 2;
}
long long countAlternatingSubarrays(vector<int>& nums) {
long long ans = 0;
for (int i=0, j=0; j<nums.size(); ) {
// j到了最后
if (j == nums.size() - 1) {
ans += A(j-i+1);
j ++;
} else if (j + 1 < nums.size()) {// j可以往后
if (nums[j] != nums[j+1]) {// j和下一位不等,继续加
j ++;
} else {// j和下一位相等,相加后继续+
ans += A(j-i+1);
i = ++j;
}
}
}
return ans;
}
};最小化曼哈顿距离
题目
给你一个下标从 0 开始的数组 points ,它表示二维平面上一些点的整数坐标,其中 points[i] = [xi, yi] 。
两点之间的距离定义为它们的曼哈顿距离
曼哈顿距离:两个单元格
(xi, yi)和(xj, yj)之间的曼哈顿距离为|xi - xj| + |yi - yj|。
请你恰好移除一个点,返回移除后任意两点之间的 最大 距离可能的 最小 值。
示例 1:
输入:points = [[3,10],[5,15],[10,2],[4,4]]
输出:12
解释:移除每个点后的最大距离如下所示:
- 移除第 0 个点后,最大距离在点 (5, 15) 和 (10, 2) 之间,为 |5 - 10| + |15 - 2| = 18 。
- 移除第 1 个点后,最大距离在点 (3, 10) 和 (10, 2) 之间,为 |3 - 10| + |10 - 2| = 15 。
- 移除第 2 个点后,最大距离在点 (5, 15) 和 (4, 4) 之间,为 |5 - 4| + |15 - 4| = 12 。
- 移除第 3 个点后,最大距离在点 (5, 15) 和 (10, 2) 之间的,为 |5 - 10| + |15 - 2| = 18 。 在恰好移除一个点后,任意两点之间的最大距离可能的最小值是 12 。 示例 2:
输入:points = [[1,1],[1,1],[1,1]]
输出:0
解释:移除任一点后,任意两点之间的最大距离都是 0 。
提示:
3 <= points.length <= 105
points[i].length == 2
1 <= points[i][0], points[i][1] <= 108
思路
需要用到一个数学技巧:曼哈顿距离转切比雪夫距离
曼哈顿距离就是
如何转换?
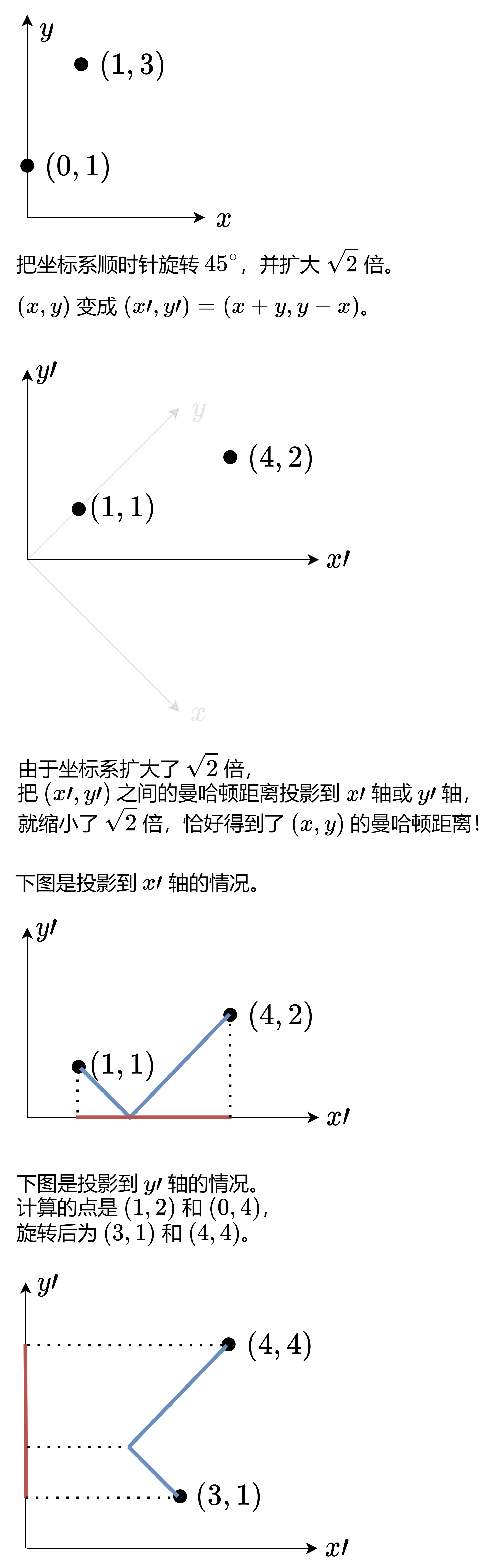
将坐标系顺时针旋转(如图1图2),此时x变成为x+y,y变成y-x,同时坐标系扩大了倍
知道这个结论有什么用?
- 原来未旋转,我们需要的是图三一样的蓝色线路,即原来的曼哈顿距离
- 当旋转了之后,坐标系扩大了倍,那么原来的蓝色线条投射到x轴上,就是除以倍
- 乘以根号二除以,所以结果不变,所以曼哈顿距离就是旋转后的x的差的绝对值
图四是其他点投影到y轴上
那么如何确定往x投影还是往y投影呢?答案是用max判断如果投影折叠了那就短了,即取两种投影的最大值
这样就可以得到公式
这就是切比雪夫距离
所以曼哈顿距离转换成了最大的x的差值和最大的y的差值
但是题目要求删去最大值,思路是维护一个有序集合,里面装x和y的差值,最后遍历一遍points数组,依次删去点,然后加回来,遍历一遍就知道结果了
代码
class Solution {
public:
int minimumDistance(vector<vector<int>> &points) {
// 有序可重复set
multiset<int> xs, ys;
for (auto &p : points) {
xs.insert(p[0] + p[1]);
ys.insert(p[1] - p[0]);
}
int ans = INT_MAX;
// 遍历所有的点
for (auto &p : points) {
int x = p[0] + p[1], y = p[1] - p[0];
// 找到下标然后删除单个点
xs.erase(xs.find(x));
ys.erase(ys.find(y));
// 找到去掉一个点后,得到min(x最大值,y最大值)
ans = min(ans, max(*xs.rbegin() - *xs.begin(), *ys.rbegin() - *ys.begin()));
// 加回单个点
xs.insert(x);
ys.insert(y);
}
return ans;
}
};参考: